오귀스탱 프레넬

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 생애
3. 과학적 업적
4. 수상 및 명예
5. 평가 및 영향
참조

1. 개요

오귀스탱 프레넬은 1788년 프랑스에서 태어난 물리학자이자 기술자이다. 그는 빛의 파동설을 확립하고, 빛의 회절, 간섭, 편광 현상을 실험적으로 증명하여 광학 연구에 크게 기여했다. 특히 빛이 횡파임을 밝혀내고, 프레넬 렌즈를 발명하여 등대 기술 발전에 혁신을 가져왔다. 그의 연구는 19세기 광학 연구의 기반을 마련하고, 제임스 클러크 맥스웰의 전자기 이론으로 이어지는 중요한 발판이 되었다.

더 읽어볼만한 페이지

등대 - 탑
탑은 산스크리트어 '스투파'에서 유래되었으며, 불교의 사리 봉안, 기념, 감시, 통신 등 다양한 목적의 높은 구조물을 통칭하며, 지구라트, 피라미드, 성의 방어 시설, 교회 건축, 송전탑 등으로 발전해왔다.
등대 - 등선
등선은 등대 건설이 어려운 해상에서 등대와 유사한 기능을 수행하는 닻으로 고정된 비자항식 폰툰으로, 부표보다 시인성이 높고 해양 관측, 기상 관측, 항행 선박 감시 등 다양한 기능을 수행하며, 현대에는 첨단 장비가 추가되어 해상 교통 안전 확보에 기여한다.
프랑스의 인도주의자 - 루이 파스퇴르
루이 파스퇴르는 1822년에 태어나 1895년에 사망한 프랑스의 생물학자이자 화학자로서, 분자 키랄성을 입증하고 생물 속생설을 확립했으며, 저온 살균법과 백신 개발을 통해 과학 발전에 크게 기여했다.
프랑스의 인도주의자 - 카트린 드뇌브
카트린 드뇌브는 프랑스의 배우로, 1960년대 초 영화에 데뷔하여 《쉘부르의 우산》으로 세계적인 스타가 되었으며, 다양한 영화에 출연하고 모델, 사업가로 활동하며, 프랑스 공화국의 마리안느 모델로도 활동했다.
프랑스의 토목공학자 - 귀스타브 에펠
프랑스의 토목기사이자 건축가인 귀스타브 에펠은 철골 구조 건축의 선구자로서 에펠탑 건설과 자유의 여신상 내부 구조 설계에 참여했으며, 후기에는 항공학 발전에도 기여했지만 파나마 운하 스캔들에 연루되기도 했다.
프랑스의 토목공학자 - 장바티스트 비오
프랑스의 물리학자이자 천문학자인 장-바티스트 비오는 광학, 전자기학, 천문학 분야에서 중요한 업적을 남겼고, 열기구 고고도 비행, 자오선 호 측량 사업 참여, 빛의 편광 연구를 통한 선광 현상 발견, 비오-사바르 법칙 발견, 운석의 우주 기원 규명 등 다양한 활동을 통해 여러 학회에서 인정받았다.

오귀스탱 프레넬 - [인물]에 관한 문서

2. 생애

프레넬은 1788년 노르망디의 브로이에서 건축가의 아들로 태어났다. 어린 시절에는 8세가 되어서야 글을 읽고 쓸 정도로 학습이 더뎠으나, 에콜 폴리테크니크와 국립 토목 학교에 진학하여 뛰어난 재능을 발휘했다. 졸업 후에는 방데주, 드롬주, 일레빌렌주 등에서 도로 건설에 참여하는 기술자로 활동하며 틈틈이 광학 실험을 수행했다.

1815년, 엘바 섬을 탈출한 나폴레옹 보나파르트가 프랑스로 돌아오자, 프레넬은 국왕 루이 18세를 지지하다가 기술자 직위를 잃고 연금 상태에 놓이기도 했다. 그러나 이 시기에 오히려 광학 연구에 몰두하여 빛의 회절 현상을 파동설로 설명하는 중요한 성과를 거두었다(프레넬 회절). 나폴레옹의 백일천하가 끝나고 루이 18세가 복위하자 프레넬도 복직하여 파리에서 기술자 업무를 재개했다.

이후에도 프레넬은 기술 업무와 광학 연구를 병행했다. 그는 편광 현상에 대한 깊이 있는 연구를 통해 빛이 진행 방향에 수직으로 진동하는 횡파라는 사실을 실험적으로 증명했다. 이는 호이겐스와 토머스 영 등이 제안했던 기존의 파동설(빛을 종파로 간주)을 보완하고 발전시킨 중요한 발견이었다. 프레넬의 이론은 복굴절과 같은 복잡한 광학 현상들을 성공적으로 설명했으며, 널리 받아들여지게 되었다. 또한 광행차에 대한 그의 연구는 훗날 마이컬슨-몰리 실험과 특수 상대성 이론으로 이어지는 중요한 기초를 제공했다. 프랑수아 아라고와 함께 광학 이론을 체계적으로 정리하여 발표했으며, 이러한 학문적 공로를 인정받아 1823년 프랑스 과학 아카데미 회원으로 선출되었고, 1824년에는 런던 왕립 학회로부터 권위 있는 럼퍼드 메달을 수상했으며 이듬해 외국인 회원으로 추대되었다^[301]。

프레넬은 이론 연구뿐만 아니라 실용적인 발명에도 기여했다. 그는 여러 개의 얇은 렌즈 조각을 동심원 형태로 배열하여 하나의 거대한 렌즈와 같은 효과를 내는 새로운 방식의 등대용 렌즈를 개발했다. 이 렌즈는 제작이 용이하고 효율이 높아 프레넬 렌즈라는 이름으로 오늘날까지도 등대를 비롯한 다양한 광학 기기에 널리 사용되고 있다.

평생 건강 문제로 고생했던 프레넬은 1827년 결핵으로 인해 39세의 젊은 나이로 세상을 떠났다.

2. 1. 초기 생애와 교육

브로이의 오귀스탱 프레넬 거리에 있는 그의 생가 외벽에 설치된 기념비. 1884년 9월 14일에 제막되었다.

오귀스탱 장 프레넬(Augustin-Jean Fresnel)은 1788년 5월 10일 노르망디 브로이에서 건축가인 아버지 자크 프레넬과 어머니 오귀스틴 메리메 사이에서 태어났다.^[5]^[6] 그는 네 아들 중 둘째였으며, 가족은 1789년경 셰르부르로,^[5] 1794년에는 아버지의 고향인 마티외로 이사했다.^[6] 형 루이는 에콜 폴리테크니크를 졸업하고 군인이 되었으나 스페인 하카 전투에서 전사했다.^[6] 동생 레오노르는^[5] 오귀스탱처럼 토목 기술자가 되어 형의 연구를 도왔고,^[8]^[9] 막내 동생 풀랑스 프레넬은 언어학자이자 외교관으로 활동했다.^[10]^[11] 외삼촌인 장 프랑수아 "레오노르" 메리메는 화가이자 에콜 데 보자르의 비서, 에콜 폴리테크니크의 교수였으며, 작가 프로스페르 메리메의 아버지이기도 하다.^[6]^[12]

프레넬 형제는 처음에 어머니에게 가정 교육을 받았다. 오귀스탱은 어릴 때 몸이 약했고 암기에는 소질이 없어 학습이 더딘 아이로 여겨졌다.^[13] 8살이 되어서야 겨우 글을 읽기 시작했다는 이야기가 전해지지만, 이는 논란의 여지가 있다.^[14] 하지만 어린 시절 나뭇가지로 성능 좋은 장난감 활과 총을 만들어 주변 아이들에게 '천재'(l'homme de génie^fra)라 불리기도 했다.^[15]

1801년, 프레넬은 형 루이와 함께 캉에 있는 중앙 학교(École Centrale^fra)에 입학하여 학업 능력을 키웠다. 1804년 말, 그는 에콜 폴리테크니크 입학 시험에서 17등으로 합격했다.^[16] 에콜 폴리테크니크 재학 시절 기록은 많이 남아있지 않지만, 계속된 건강 문제에도 불구하고 그림과 기하학에서 두각을 나타냈으며,^[17] 첫 해에는 아드리앵마리 르장드르가 낸 기하학 문제 풀이로 상을 받기도 했다.^[18] 1806년에 졸업한 후, 국립 토목 학교(École Nationale des Ponts et Chaussées, ENPC)에 진학하여 1809년에 졸업했다. 졸업 후 그는 교량 및 도로 공무단(Corps des Ponts et Chaussées)에 수습 엔지니어(ingénieur ordinaire aspirant^fra)로 임명되어 평생 이 분야에서 일하게 된다.^[19]

2. 2. 종교적 배경

프레넬의 부모는 얀센주의 분파 로마 가톨릭교회 신자였다. 얀센주의는 아우구스티누스의 사상을 바탕으로 원죄 교리를 특히 강조하는 경향이 있었다. 종교는 프레넬 형제들의 가정 교육에서 매우 중요한 부분을 차지했다. 1802년 그의 어머니는 "나는 내 아들이 자신이 받은 훌륭한 재능을 자신의 이익과 만물의 신을 위해 사용할 수 있도록 은총을 주시기를 하느님께 기도합니다. 많은 것을 받은 자에게 많은 것이 요구될 것이며, 더 많은 것을 받은 자에게는 더 많은 것이 요구될 것입니다."^[20]라고 말하며 종교적 신념에 기반한 교육관을 드러냈다.

오귀스탱 프레넬 자신도 얀센주의자로 남았다.^[21] 그는 자신의 뛰어난 지적 능력을 신이 주신 선물로 여겼으며, 이를 다른 사람들을 위해 사용하는 것을 자신의 의무라고 생각했다.^[22] 그의 동료 기술자였던 알퐁스 듈로(Alphonse Duleau)는 프레넬이 자연을 연구하는 것을 신의 힘과 선함을 알아가는 과정의 일부로 보았다고 전했다. 프레넬은 미덕을 과학적 재능이나 천재성보다 더 중요하게 여겼으며, 마지막 병상에서는 죽음뿐만 아니라 "유용한 적용을 얻기를 바랐던 발견의 중단"을 막기 위해 "영혼의 강인함"을 달라고 기도했다고 한다.^[23]

얀센주의는 당시 로마 가톨릭 교회 내에서 이단으로 간주되기도 했는데, 일부 연구자(그라탄-기네스)는 이것이 프레넬이 안정적인 학계 직위를 얻지 못한 이유일 수 있다고 주장한다.^[24] 실제로 그의 유일한 교직 경험은 1819년부터 1820년 겨울까지 아테네에서 잠시 가르친 것뿐이었다.^[25] 한편, ''가톨릭 백과사전''의 프레넬 항목에서는 그의 얀센주의 신앙에 대한 직접적인 언급 없이, 그를 "깊이 종교적이며 예리한 의무감을 가진 사람"으로 묘사하고 있다.

2. 3. 기술자로서의 경력

1809년 국립 토목 학교(ENPC)를 졸업한 후, 프레넬은 교량 및 도로 공무단에 ''ingénieur ordinaire aspirant''(수습 엔지니어)로 합류하여 평생 동안 직간접적으로 이 기관에 소속되었다.^[19] 그는 방데주, 드롬주, 일레빌렌주 등 프랑스 여러 지역에서 기술자로 근무하며 도로 건설과 같은 토목 공사에 참여했다.

처음에는 서부 방데주에 배치되었다. 1811년 그곳에서 프레넬은 암모니아 재활용 과정을 고려하지 않았다는 점을 제외하면, 훗날 탄산나트륨 생산을 위한 솔베이 공정으로 알려지게 된 것을 예측했다. 이 차이 때문에 그의 삼촌 레오노르를 통해 이 발견을 알게 된 주요 화학자들은 결국 경제성이 없다고 판단하게 되었다.^[26]

1812년경, 프레넬은 드롬주 남부의 뉘옹으로 이동하여 스페인과 이탈리아를 연결하는 제국 고속도로 건설을 도왔다.^[6] 뉘옹에서 그는 광학에 대한 관심을 처음으로 드러내기 시작했다. 1814년 5월 15일, 나폴레옹의 패배로 업무가 한가해진 틈을 타,^[27] 그는 형 레오노르에게 보낸 편지에서 빛의 편광에 대한 논문을 구하고 싶다는 뜻을 밝혔다.^[28]

1815년 3월, 엘바 섬에서 돌아온 나폴레옹의 복귀를 "문명에 대한 공격"으로 여긴 프레넬은^[30] 왕당파를 지지하기 위해 무단으로 근무지를 이탈하여 툴루즈로 향했으나 곧 병가를 냈다. 나폴레옹이 패배한 후 뉘옹으로 돌아왔지만 협박을 당하고 집 창문이 깨지는 일을 겪었다. 백일천하 동안 그는 정직 처분을 받았고, 결국 고향 마티외의 어머니 집에서 지내게 되었다.^[31] 이 시기 그는 강제로 얻게 된 여가 시간을 활용하여 광학 실험에 몰두했다.

나폴레옹의 백일천하가 끝나고 루이 18세가 다시 왕위에 오르자 프레넬은 복직하여 파리에서 기술자로서의 업무를 재개했다. 이후에도 그는 기술자로서의 업무와 광학 연구를 병행했다.

2. 4. 광학 연구

1812년경, 프레넬은 스페인과 이탈리아를 잇는 제국 고속도로 건설을 돕기 위해 드롬주 남부의 뉘옹으로 파견되었다.^[6] 이곳에서 그는 광학에 대한 관심을 처음으로 드러냈다. 1814년 5월 15일, 나폴레옹의 패배로 업무가 한가해지자,^[27] 프레넬은 형 레오노르에게 보낸 편지의 추신에서 빛의 편광에 대한 논문을 구하고 싶다고 적으며, 장바티스트 비오가 발표한 편광 관련 논문에 대해 궁금해했다.^[28] 그는 1815년 2월 10일경 비오의 논문을 받아볼 수 있었다.^[29]

1815년 3월, 엘바 섬에서 탈출한 나폴레옹의 복귀를 "문명에 대한 공격"으로 여긴 프레넬은^[30] 무단으로 근무지를 이탈하여 툴루즈에서 왕당파 저항군에 합류하려 했으나 병으로 인해 뜻을 이루지 못했다. 뉘옹으로 돌아온 그는 위협을 받았고, 백일천하 동안 정직 처분을 받아 마티외에 있는 어머니의 집으로 가게 되었다. 프레넬은 이 강제 휴가 기간을 활용하여 광학 실험에 몰두하기 시작했다.^[31] 그는 이 시기에 빛의 회절 현상을 빛의 파동설로 설명할 수 있음을 증명했다(프레넬 회절). 나폴레옹 실각 후 루이 18세가 복위하자 프레넬도 복직하여 파리에서 기술자로 일하게 되었다.

이후에도 프레넬은 업무와 병행하며 광학 연구를 계속했다. 호이겐스와 토머스 영 등이 주장한 기존의 파동설에서는 빛을 음파처럼 종파로 간주했다. 그러나 프레넬은 편광 현상을 연구하면서 빛이 진행 방향에 수직으로 진동하는 횡파라는 결론에 도달했다.

1816년 8월 30일자 초고 논문에서 프레넬은 앙드레마리 앙페르에게서 비롯된 아이디어, 즉 편광된 빛 파동이 부분적으로 횡파일 경우 직교 편광된 빛이 간섭하지 않는 현상을 설명할 수 있다는 가설을 언급했다. 그러나 그는 이를 완전한 이론으로 발전시키지는 못했다. 같은 해 9월 초부터 그는 직교 편광된 빛의 비간섭성과 색 편광에서의 위상 반전 규칙이 빛이 '순수하게' 횡파일 경우 가장 잘 설명된다는 점을 깨달았다. 앙페르 역시 위상 반전 규칙에 대해 같은 생각을 가지고 있었다. 하지만 자연광은 편광되지 않은 것처럼 보였기에, 당시에는 종파로 추정되던 빛의 진동에서 어떻게 종파 성분이 사라지는지, 그리고 편광된 빛이 비스듬히 반사되거나 굴절될 때 왜 종파 성분이 다시 나타나지 않는지를 설명해야 하는 새로운 난관에 부딪혔다.^[160]^[161]

한편, 1817년 1월 12일, 토머스 영은 아라고에게 보낸 편지에서 횡 진동이 편광을 구성하며, 두 종파가 상당한 각도로 교차하면 횡 진동 성분 없이는 소멸될 수 없다고 제안했다.^[162] 영은 1818년 브리태니커 백과사전 부록에 실린 논문에서 이 아이디어를 다시 언급하며, 편광이 횡 운동으로 이루어진다면 말루스의 법칙이 설명될 것이라고 덧붙였다.

프레넬이 빛 파동이 횡 성분을 가질 수 있다거나 편광된 파동이 전적으로 횡파일 수 있다고 처음 의심한 사람은 아닐 수 있으며, 편광이 횡 진동 방향에 달려있다는 생각을 처음 발표한 것은 영이었다. 그러나 이러한 초기 이론들은 편광의 본질과 비편광된 빛의 존재를 조화시키지 못했다. 이 문제를 해결한 것은 프레넬이었다.

1818년 여름으로 추정되는 메모에서 프레넬은 비편광 파동이 파동의 법선에 대해 균일하게 분포된 방향을 가진 동일한 에너지의 사선 진동으로 구성될 수 있으며, 편광의 정도는 분포의 불균일성 정도에 해당한다는 아이디어를 탐구했다. 그는 또한 위상 반전 규칙과 직교 편광된 빛의 비간섭성이 완전히 편광된 파동의 진동이 순수하게 횡파일 경우 쉽게 설명될 것이라고 언급했다.^[163]

횡 성분의 평균으로 편광 부족을 설명할 수 있다면, 종파 성분을 가정할 필요가 없었다. 빛 파동이 순수하게 횡파여서 특정 횡 방향을 가지며 항상 편광되어 있고, 자연광의 '비편광' 상태는 방향의 빠르고 무작위적인 변화 때문이라고 가정하면 충분했다. 이 경우, '비편광된' 빛의 두 간섭성 부분은 방향이 동기화되어 여전히 간섭할 수 있었다.

프레넬이 언제 이 최종 단계에 도달했는지는 정확히 알려지지 않았으나,^[164] 그는 1821년 5월, 6월, 7월호 아라고의 ''Annales''에 연재된 Calcul des teintes…|색 계산…^프랑스어에 관한 논문에서 이 아이디어를 처음 발표했다.^[165] 첫 부분에서 그는 '직접'(비편광된) 빛을 "모든 방향으로 편광된 파동 시스템의 빠른 연속"으로 묘사하고,^[166] 색 편광을 힘의 분해 유추를 통해 설명하며 횡파는 각주에서만 언급했다. 횡파 개념은 두 번째 부분에서 본격적으로 도입되었는데, 그는 자신과 앙페르가 1816년부터 가졌던 의심과 그로 인한 어려움을 설명했다.^[167] 그는 "직접 광선뿐만 아니라 편광된 광선의 빛 파동 진동 운동이 오직 이러한 파동의 평면을 따라 수행된다는 것을 깨달은 지 불과 몇 달밖에 되지 않았다"고 밝혔다.^[168]^[169] 이 새로운 관점에 따르면, "편광의 행위는 횡 운동을 생성하는 것이 아니라, 이를 두 개의 고정된 수직 방향으로 분해하고 두 성분을 분리하는 것"이었다.^[170]

이러한 프레넬의 편광 이론은 빛의 입자설(선택론)로는 설명하기 어려웠다. 입자설에서 편광 상태는 입자 집단의 정적인 방향 분포와 관련되었지만, 프레넬에게 편광 상태는 시간에 따른 변위의 변화와 관련되었기 때문이다. 파동 이론과 입자설 사이의 간극은 더욱 벌어졌다.^[171] 순수 횡파 이론은 빛을 전달하는 매질인 에테르가 탄성 고체처럼 행동해야 한다는 점, 그러면서도 종파는 전달하지 못한다는 모순적인 가정을 내포하는 어려움이 있었다.^[172]^[173]

=== 프레넬 방정식 ===

1821년 6월 발표된 논문의 두 번째 부분에서 프레넬은 소리 파동과의 유추를 통해, 굴절 매질 내 에테르 밀도가 파동 속도의 제곱에 반비례하고 굴절률의 제곱에 정비례한다고 가정했다. 그는 서로 다른 굴절률을 가진 두 등방성 매질 사이의 경계면에서 반사와 굴절을 설명하기 위해, 횡 진동을 입사면에 수직인 성분(''s'' 성분)과 평행한 성분(''p'' 성분)으로 분해했다.^[174] ''s'' 성분에 대해 그는 두 매질 간의 상호작용을 탄성 충돌과 유사하다고 가정하고, 반사된 강도와 입사 강도의 비율인 반사율 공식을 유도했다. 이 공식에 따르면 반사율은 모든 각도에서 0이 아니었다.^[175]

1821년 7월 발표된 세 번째 부분의 추신에서 프레넬은 "기계적 해법"을 통해 ''p'' 성분의 반사율 공식을 발견했으며, 이 공식은 특정 각도(브루스터 각)에서 반사율이 0이 됨을 예측한다고 발표했다. 이는 반사에 의한 편광 현상을 설명해주었지만, 프레넬 모델의 진동 방향이 말루스가 정의한 편광면에 수직이어야 한다는 조건이 따랐다. 당시 기술로는 임의의 입사각에서 ''s'' 및 ''p'' 반사율을 정확히 측정하여 프레넬 공식을 검증하기 어려웠다. 그러나 반사된 진폭과 입사 진폭의 비율인 반사 계수를 이용하여 이론을 검증할 수 있었다. 입사광의 편광면이 입사면에 대해 45°일 때, 반사광의 편광 각도는 두 반사 계수의 비율로부터 계산될 수 있었고, 프레넬은 유리와 물에 대해 다양한 입사각에서 이 각도를 측정하여 계산값과 측정값 사이의 오차가 1.5° 이내임을 확인했다.^[176]

프레넬은 1823년 1월 7일 과학 아카데미에서 발표한 논문에서 "기계적 해법"의 세부 사항을 제시했다. 그는 에너지 보존 법칙과 경계면에서 접선 방향 진동의 연속성을 결합하여^[177] 반사 계수와 반사율에 대한 공식을 유도했는데, 이것이 바로 ''프레넬 방정식''이다. ''s'' 및 ''p'' 편광에 대한 반사 계수는 다음과 같다.

:

r_s=-\frac{\sin(i-r)}{\sin(i+r)}

및

r_p=\frac{\tan(i-r)}{\tan(i+r)}\,,

여기서 ''i''와 ''r''은 각각 입사각과 굴절각이다. 이들은 각각 ''프레넬의 사인 법칙'' 및 ''프레넬의 탄젠트 법칙''으로 알려져 있다.^[178] 프레넬은 반사 계수를 복소수로 확장하여 전반사 시 ''s'' 및 ''p'' 성분 사이에 발생하는 위상차까지 설명했다.^[179] 프레넬 방정식은 이후 제임스 맥컬러와 오귀스탱 루이 코시 등이 금속 반사를 분석하는 데 영감을 주었으며,^[180] 현대 컴퓨터 그래픽스의 물리 기반 렌더링 등 다양한 분야에서 활용되고 있다.

=== 원형 편광과 타원 편광, 광학 회전 ===

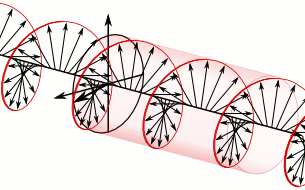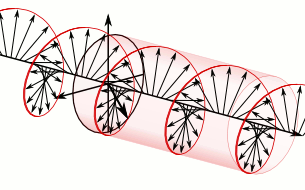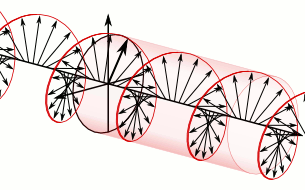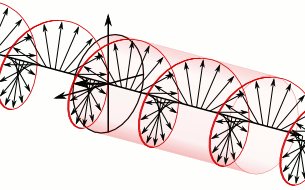
오른손/시계 방향 원편광 파동 (광원 기준). 수신기 기준으로는 왼손/반시계 방향 원편광으로 간주된다. 회전 벡터의 수평 및 수직 성분은 1/4 주기 위상차를 가진다.

1822년 12월 9일 작성된 회고록에서 프레넬은 편광의 종류를 세분화했다. 그는 진동의 수직 성분들이 같은 위상이거나 180° 위상차를 가질 때 ''polarisation rectiligne|선형 편광^프랑스어'', 크기가 같고 1/4 주기(±90°) 위상차를 가질 때 ''원형 편광'', 그 외 고정된 진폭비와 위상차를 가질 때 ''타원 편광''이라는 용어를 만들었다. 그는 또한 광학 회전 현상이 복굴절의 한 종류로 이해될 수 있음을 설명했다. 선형 편광된 빛을 서로 반대 방향으로 회전하는 두 개의 원형 편광 성분으로 분해할 수 있는데, 만약 이 두 성분이 매질 내에서 약간 다른 속도로 전파된다면 그들 사이의 위상차가 계속 변하게 되고, 결과적으로 합성된 선형 편광의 방향이 거리에 따라 회전하게 된다는 것이다.^[181]

이러한 개념들은 편광된 빛과 비편광된 빛의 구분을 새롭게 정의할 필요성을 제기했다. 프레넬 이전에는 편광의 정도는 변할 수 있어도 종류는 변하지 않는다고 생각했다. 따라서 선형 편광이 결정 박편 통과나 전반사 등으로 타원 편광이나 원형 편광으로 변환된 빛은 부분적으로 또는 완전히 "비편광"된 것으로 간주되었다. 프레넬 이후, 편광된 빛은 수직 진동 성분들이 고정된 진폭비와 위상차를 갖는 것으로 정의되었고, 이에 따라 타원 편광이나 원형 편광된 빛도 완전히 편광된 것으로 간주되었다.^[182]

=== 프레넬 롬버스 ===

프레넬 롬버스(청색) 단면도. 입사면에 평행한 ''p'' 성분(수직축)과 수직인 ''s'' 성분(수평축)을 보여준다. 선형 편광된 입사광(위)은 롬버스 내부에서 두 번 반사되면서 ''p'' 성분과 ''s'' 성분 사이에 위상차가 발생하여(중간, 아래) 타원 편광 또는 원형 편광(초기 ''s'', ''p'' 성분 크기가 같을 경우)으로 변환된다.

1817년경 데이비드 브루스터는 평면 편광된 빛이 전반사될 때 부분적으로 편광이 풀리는 현상을 발견했다.^[183] 프레넬은 이 효과를 재발견하고, 전반사가 입사면에 평행한 성분과 수직인 성분 사이에 위상차를 도입한다는 것을 밝혀냈다.^[184] 그는 특정 입사각에서 두 번의 전반사를 이용하면 1/4 주기(90°)의 위상차를 만들 수 있음을 발견하고, 이를 구현하기 위해 유리 평행육면체 모양의 장치, 즉 ''프레넬 롬버스''를 고안했다. 프레넬 롬버스는 선형 편광된 빛을 원형 또는 타원 편광된 빛으로 변환하는 데 사용될 수 있다.

1818년 1월의 부록에서 프레넬은 프레넬 롬버스와 복굴절 판을 조합하여 광학 회전을 인공적으로 모방할 수 있음을 보고했다.^[185] 3월 30일 발표된 논문에서는^[186] 프레넬 롬버스를 통과하여 원형 편광(프레넬의 용어로는 완전히 "탈편광")된 빛은 이후 광학 활성 매체를 통과해도 더 이상 특성이 변하지 않는다고 보고했다. 1823년 1월 논문에서는 전반사 시 발생하는 위상 변화를 정량화하고, 굴절률 1.51인 유리로 프레넬 롬버스를 만들 경우 선형 편광을 원형 편광으로 변환하기 위한 최적의 각도가 약 48.6° 또는 54.6°임을 계산했다.

=== 복굴절 ===

방해석과 같은 단축성 결정의 복굴절은 호이겐스의 이론으로 설명될 수 있었지만, 토파즈와 같은 이축성 결정의 더 복잡한 복굴절 현상은 설명하기 어려웠다. 1819년 비오는 이축성 결정에 대한 광선 속도 법칙('비오의 사인 법칙')과 편광 법칙('비오의 이면각 법칙')을 발표했지만,^[191] 이는 근사적인 것이었다.

1821년 11월 19일 제출된 논문에서,^[195] 프레넬은 토파즈 실험을 통해 이축성 결정에서는 두 개의 굴절된 광선 모두 스넬의 법칙을 따르지 않음을 보였다. 즉, 어떤 광선도 구형 파면을 형성하지 않는다는 것이다.^[196] 같은 논문에서 그는 이축성 결정의 광선 속도를 설명하기 위해 3축 타원체 모델을 제안하고, 이를 통해 비오의 사인 법칙을 유도했다.^[197]^[198] 그러나 이 모델은 진동 방향을 정확하게 예측하지 못했다. 일주일 후인 11월 26일 발표에서 프레넬은 파면에 접선 방향으로 진동한다는 점을 고려하여 파동-법선 속도와 진동 방향을 설명하는 4차 방정식 형태의 "탄성 표면" 개념을 도입했다. 그는 초기 타원체 모델을 근사치로 사용하여 비오의 이면각 법칙을 유도했다.^[199]

1822년 1월 부록에서 프레넬은 탄성 표면의 "기계적" 유도를 시도했고,^[200] 3월에 제출된 "두 번째 부록"에서는^[203] 이축성 결정에서 빛의 파면("파동 표면")을 설명하는 4차 방정식을 유도하는 데 성공했다.

: ''r''²(''a''²''x''² + ''b''²''y''² + ''c''²''z''²) − ''a''²(''b''² + ''c''²)''x''² − ''b''²(''c''² + ''a''²)''y''² − ''c''²(''a''² + ''b''²)''z''² + ''a''²''b''²''c''² = 0

여기서 ''r''² = ''x''² + ''y''² + ''z''² 이고, ''a'', ''b'', ''c''는 주축 방향으로 진동하는 빛의 전파 속도이다.^[204] 이 방정식은 후에 다음과 같은 더 간결한 형태로 표현되었다.

: ''x''²/(''r''²−''a''²) + ''y''²/(''r''²−''b''²) + ''z''²/(''r''²−''c''²) = 1

또한 프레넬은 매질을 점-질량 배열로 모델링하여 변위와 힘의 관계가 대칭 행렬로 표현됨을 보였고, 이를 통해 변위와 평행한 힘을 생성하는 세 개의 수직 축이 존재함을 이론적으로 뒷받침했다.^[205] 그는 이축성 결정에서는 파동-법선 속도가 단일한 방향(광축)과 광선 속도가 단일한 방향(광선축)이 일반적으로 일치하지 않음을 지적했다.^[206]

프레넬은 1824년 아카데미에 제출하여 사후인 1827년에 출판된 복굴절에 관한 "두 번째 논문"^[209]에서 자신의 이론을 기계적 기초를 중심으로 재정리하고, 비오의 이면각 법칙이 파동 법선 방향을 기준으로 할 때 정확함을 엄밀하게 증명했다.^[207]^[208]^[211]^[212]^[213] 프레넬의 연구는 오귀스탱 루이 코시에게 영향을 주어 비등방성 고체 탄성 이론과 그 안에서의 횡파 이론 발전에 기여했다.^[214] 프레넬의 모델 자체는 역학적으로 완벽하지 않았지만, 그의 파동 이론은 입자설로는 불가능했던 방식으로 광범위한 광학 현상을 설명하고 예측하는 강력한 도구를 제공했다.^[216]

=== 광탄성 및 원형 복굴절 ===

1815년 브루스터는 등방성 물질에 기계적 응력을 가하면 복굴절이 유발되어 편광판 사이에서 색깔이 나타나는 현상(광탄성)을 발견했다. 프레넬은 1822년 9월 발표에서 여러 개의 프리즘을 압축하여 실제로 이중 상을 관찰함으로써 브루스터의 설명을 직접적으로 확인했다. 그의 실험에서 프레넬은 7개의 45°–90°–45° 프리즘을 정렬하고 압축했을 때, 물체가 수직 편광된 두 개의 이미지로 보였으며, 그 간격은 1미터 거리에서 1.5mm였다.^[217]

같은 논문에서 프레넬은 압축된 유리 대신 광학 활성이 있는 석영 프리즘을 사용하면, 광축 방향으로 볼 때 두 개의 이미지가 생성될 것이라고 예측했다. 이 이미지들은 원형 편광 상태일 것이며, 이는 광학 회전이 복굴절의 한 형태임을 보여주는 증거가 된다. 1822년 12월 논문에서 그는 실제로 석영 프리즘을 이용하여 이 예측을 실험적으로 확인했으며, 이를 통해 광학 회전이 서로 반대 방향으로 원형 편광된 빛의 속도 차이에 의해 발생한다는 자신의 이론을 증명했다.^[218]

프레넬의 광학 연구는 빛의 본성에 대한 이해를 근본적으로 바꾸었으며, 그의 이론과 공식들은 오늘날까지도 광학 분야의 기초를 이루고 있다. 그의 연구는 1818년 프랑스 과학 아카데미 그랑프리 수상, 1823년 프랑스 과학 아카데미 회원 선출, 1824년 런던 왕립 학회 럼퍼드 메달 수상, 1825년 왕립 학회 외국인 회원 선출 등으로 이어졌다.^[301]

2. 5. 등대와 프레넬 렌즈

프레넬이 렌즈를 사용하여 등대 빔의 초점을 맞춘 첫 번째 인물은 아니었다. 런던의 유리 세공인 토마스 로저스는 1789년 포틀랜드 빌의 올드 로어 등대에 처음으로 렌즈(직경 53cm, 중앙 두께 14cm)를 설치했지만, 당시 기술로는 유리에 의한 빛 흡수가 많아 효율이 떨어졌다.^[238]

또한, 볼록 렌즈를 여러 개의 동심 환형 프리즘으로 나누어 무게와 빛 흡수를 줄이자는 아이디어도 프레넬이 처음 제안한 것은 아니었다. 1748년 뷔퐁 백작은 단일 유리 조각에서 단계적으로 프리즘을 연마하는 방식을 제안했고, 1790년 콩도르세 후작은 각 환형 부분을 별도로 제작하여 조립하는 방식을 제안했다.^[240] 하지만 이 디자인들은 태양광선 집광기를 위한 것이었고 당시 기술로는 실용적이지 않았다. 데이비드 브루스터 역시 1811년에 유사한 시스템을 제안하고 1820년까지 영국 등대에 사용할 것을 주장했다.

1819년 6월 21일, 프레넬은 프랑수아 아라고의 추천으로 등대 조명 개선 가능성을 검토하기 위해 '등대 위원회'(Commission des Phares)에 임시로 파견되었다.^[241] 프레넬은 이전의 제안들을 알지 못한 채, 1819년 8월 말 위원회에 기존의 반사경을 대체할 '단계별 렌즈'(lentilles à échelons^프랑스어)를 제안했다.^[243]^[244]^[245] 위원 중 한 명인 자크 샤를이 뷔퐁의 제안을 언급하자 프레넬은 당황했지만, 자신의 설계는 뷔퐁의 양볼록 단일 렌즈와 달리 평볼록 형태이며 여러 프리즘으로 분리 제작하여 더 실용적임을 강조했다.^[239]

프레넬은 공식 예산 500FRF으로 제작자를 찾아 나섰고, 프랑수아 솔레이가 1820년 3월에 첫 프로토타입을 완성했다. 55cm 크기의 사각형 패널에 97개의 다각형 프리즘을 결합한 이 렌즈는 위원회에 깊은 인상을 주었고, 프레넬은 더 큰 8개 패널 버전을 제작하라는 요청을 받았다. 자금 부족에도 불구하고 1년 후 완성된 이 모델은 76cm 크기의 패널을 가졌으며, 1821년 4월 13일 공개 시연에서 기존 반사경을 압도하는 성능을 보여주었다.^[246]

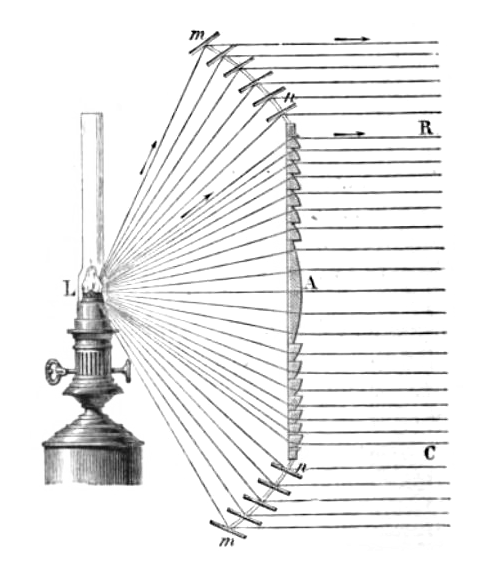
초기 프레넬 등대 렌즈의 단면도. 굴절 패널 ''RC''(중앙 세그먼트 ''A'') 위와 아래에 경사진 거울 ''m, n''. 램프 ''L''을 통과하는 모든 수직면의 단면이 동일하면 빛이 수평선 주변에 고르게 퍼진다.

프레넬의 다음 작업은 생고뱅에서 제작한 8개의 '불스아이' 패널을 갖춘 회전식 등대 렌즈였다.^[240] 이 장치는 8개의 회전하는 광선 빔을 만들어 선원들이 주기적인 섬광으로 등대의 위치를 파악할 수 있게 했다. 각 주 패널 위에는 더 작고 경사진 보조 패널과 평면 거울을 설치하여 빛을 수평으로 반사시켜 주 빔보다 약간 앞서 비추게 함으로써 섬광의 지속 시간을 늘렸다.^[247] 주 패널 아래에는 128개의 작은 거울을 여러 겹으로 배열하여 빛을 수평선 방향으로 반사시켜 섬광 사이에 희미하지만 지속적인 빛을 제공했다. 1822년 8월 20일, 미완성된 개선문 꼭대기에서 공식 테스트가 진행되었고, 루이 18세와 그의 수행원들이 32km 떨어진 곳에서 그 성능을 확인했다. 이 장치는 보르도에서 겨울을 보낸 후 프레넬의 감독 하에 코르두앙 등대에 설치되어, 1823년 7월 25일 세계 최초의 프레넬 렌즈 등대로서 불을 밝혔다.^[248] 그러나 이 시기 프레넬의 건강은 악화되기 시작했다.^[249]

1824년 5월, 프레넬은 등대 위원회의 정식 비서로 승진하여 급여를 받는 첫 위원이 되었으며, 수석 엔지니어 역할도 겸임했다.^[250]^[251] 그는 건강 악화와 등대 작업에 집중하기 위해 1821년부터 맡아왔던 에콜 폴리테크니크의 시험관 직책을 1824년 말 사임했다.^[252]

같은 해, 프레넬은 빛을 수평선 주위로 고르게 퍼뜨리면서 상하 방향으로의 빛 손실을 최소화하는 고정식 렌즈를 설계했다. 이상적인 형태는 수직축을 중심으로 회전하는 토러스 단면 모양의 렌즈였지만, 제작의 어려움 때문에 실제로는 다각형 단면으로 제작되었다.^[253] 이 설계에 기반한 최초의 3등급 고정 렌즈는 1825년 2월 1일 던커크 등대에 설치되었으며, 16각형 구조를 가졌다.^[254]^[255]

1825년, 프레넬은 고정식 렌즈 외부에 회전식 배열을 추가하는 설계를 고안했다. 이 방식은 고정된 빛의 일부를 회전하는 패널을 통해 좁은 빔으로 집중시켜 보내는 방식이었다.^[256] 또한 같은 해에 프레넬은 '등대 지도'(Carte des Phares^프랑스어)를 공개하여, 프랑스 해안의 51개 등대와 항구 조명을 렌즈 크기(등급)와 섬광 특성(고정광, 분당 1회 섬광, 분당 2회 섬광 등)에 따라 체계적으로 분류했다.^[257]

1870년 제작된 1등급 회전 카타디옵트릭 프레넬 렌즈. 파리 해군 박물관 소장. 디옵트릭(굴절) 프리즘과 카타디옵트릭(반사굴절) 프리즘이 결합되어 회전당 4번의 순수한 섬광을 만든다. 높이 , 무게 약 .

1825년 말, 프레넬은 렌즈 시스템에서 반사로 인한 빛 손실을 더욱 줄이기 위해, 기존의 거울 대신 전반사 원리를 이용하는 '카타디옵트릭'(catadioptric, 반사굴절) 프리즘을 사용할 것을 제안했다.^[259] 이 프리즘은 빛이 첫 번째 표면에서 굴절되고, 두 번째 표면에서 전반사된 후, 세 번째 표면을 통해 다시 굴절되어 나가는 방식이다. 이것이 오늘날 우리가 아는 프레넬 등대 렌즈의 기본 구조가 되었다. 프레넬은 1826년에 작은 모델을 제작했지만, 실제 크기의 카타디옵트릭 렌즈가 완성되는 것을 보지 못하고 1827년 사망했다.

프레넬 사후에도 그의 아이디어는 계속 발전했다. 스코틀랜드 엔지니어 앨런 스티븐슨은 레오노르 프레넬(오귀스탱의 동생)의 지시에 따라 최초의 토로이드 형태 고정 렌즈를 설계했고, 이는 1836년 메이 섬 등대에 설치되었다.^[260] 최초의 대형 카타디옵트릭 렌즈는 1842년 그라블린과 일 비에르주 등대를 위해 제작된 3등급 고정 렌즈였다. 최초의 완전한 1등급 카타디옵트릭 렌즈는 1852년 알리(Ailly) 등대에 설치되었으며, 순수하게 회전하는 빔을 가진 최초의 1등급 카타디옵트릭 렌즈는 1854년 생클레망데발렌 등대에 설치되어 프레넬이 구상했던 등대 시스템 계획의 완성을 보여주었다.^[261]

한편, 뷔퐁이 처음 구상했던 것과 유사한 단일 조각의 계단식 렌즈 생산은 1852년 코닝의 존 L. 길릴랜드가 프레스 성형 유리 기술 특허를 얻으면서 실용화되었다. 1950년대 이후에는 플라스틱 소재가 유리를 대체하면서, 매우 얇고 미세한 계단을 가진 프레넬 렌즈가 오버헤드 프로젝터의 집광판이나 저렴한 시트형 돋보기 등으로 널리 사용되게 되었다.^[262]

2. 6. 말년과 사망

프레넬은 평생 건강이 좋지 않았는데, 특히 1822년에서 1823년으로 넘어가는 겨울에 건강이 크게 악화되었다. 이로 인해 브리태니커 백과사전에 편광과 복굴절에 관한 기사를 기고하려던 계획을 포기해야 했다.^[269] 하지만 건강 악화 속에서도 원형 및 타원 편광, 광학 회전에 관한 논문과 프레넬 방정식의 상세한 유도 및 전반사 적용에 관한 중요한 논문들을 발표했다. 곧 그의 병이 결핵이라는 사실이 밝혀졌다.^[249]

1824년, 프레넬은 건강을 위해 활동을 줄여야 한다는 의사의 조언을 받았다. 그는 등대 관련 작업을 가장 중요한 임무로 여기고 에콜 폴리테크니크의 시험관직을 사임했으며, 기초 과학 연구 노트를 닫았다.^[249] 1825년 6월 13일, 아카데미에 제출한 그의 마지막 공식 기록은 최초의 복사계를 설명하고 관찰된 반발력이 온도 차이 때문이라고 설명하는 내용이었다.^[270]

기초 연구는 중단했지만, 자신의 파동 이론을 옹호하는 활동은 계속했다. 1826년 8월 또는 9월에는 존 허셜이 제기한 파동 이론에 대한 질문에 답하는 시간을 가졌다.^[271] 허셜은 프레넬을 왕립 학회의 럼포드 메달 수상자로 추천하기도 했다.^[272]

1826년에서 1827년으로 넘어가는 겨울, 프레넬의 기침이 더욱 심해져 봄에는 고향 마티외로 돌아갈 수 없을 정도로 병세가 악화되었다. 그가 아카데미 회의에 마지막으로 참석한 것은 1827년 4월 30일이었다. 6월 초, 그는 파리에서 서쪽으로 약 12km 떨어진 빌 다브레로 요양을 떠났고, 어머니가 그곳으로 와서 간호했다. 7월 6일, 아라고가 직접 찾아와 럼포드 메달을 전달했다. 아라고가 슬퍼하는 것을 본 프레넬은 "가장 아름다운 왕관도 친구의 무덤에 놓일 때는 아무 의미가 없다"고 속삭였다고 전해진다. 프레넬은 왕립 학회에 감사의 답을 할 기력조차 없었다. 그는 결국 8일 뒤인 1827년 7월 14일, 바스티유의 날에 39세의 젊은 나이로 세상을 떠났다.^[273]

프레넬의 유해는 파리의 페르 라셰즈 묘지에 안장되었다. 그의 묘비에는 "프랑스 학술원 회원인 오귀스탱 장 프레넬의 기념을 위하여"라는 문구가 새겨져 있으나, 세월이 흘러 일부가 마모되었다.

3. 과학적 업적

오귀스탱 프레넬은 19세기 프랑스의 물리학자로, 특히 광학 분야에서 중요한 업적을 남겼다. 그는 빛의 파동설을 수학적으로 정립하고 실험적으로 증명하는 데 결정적인 기여를 했으며, 회절, 간섭, 편광 등 다양한 광학 현상을 파동 이론으로 성공적으로 설명했다. 또한, 등대 기술에 혁신을 가져온 프레넬 렌즈를 발명하여 해상 안전에 크게 기여했으며, 이 외에도 광탄성, 에테르 끌림 가설, 분산 등 여러 물리 현상에 대한 중요한 연구를 수행했다.

3. 1. 빛의 파동 이론 확립

프레넬은 1812년경 드롬주 뉘옹에서 스페인과 이탈리아를 잇는 제국 고속도로 건설을 도우면서 광학에 대한 관심을 처음 드러냈다. 1814년 5월, 나폴레옹의 패배 후 일이 한가해지자 그는 형에게 보낸 편지에서 빛의 편광에 대한 비오의 논문을 구하고 싶다는 뜻을 밝혔다.^[28]^[29]

백일천하 동안 왕당파를 지지하다 정직 처분을 받고 고향 마티외에 머물게 된 프레넬은 이 시간을 활용하여 광학 실험에 착수했다.^[31] 그는 아라고가 추천한 그리말디, 뉴턴, 영 등의 기존 연구를 접하기 어려운 환경이었지만,^[75]^[76] 꿀 방울로 만든 점 광원과 직접 제작한 마이크로미터 등 조악한 장비로 독자적인 실험을 진행했다.^[77] 그는 스크린 대신 렌즈와 마이크로미터를 사용하여 공간에서 직접 간섭 무늬를 관찰하는 새로운 방식을 고안하여 더 정확한 측정을 가능하게 했다.^[78]

1815년 10월, 프레넬은 프랑스 학술원에 제출한 논문에서 와이어 그림자에서 나타나는 외부 및 내부 간섭 무늬를 분석했다. 그는 영과 마찬가지로 한쪽 빛을 가리면 내부 간섭 무늬가 사라지는 것을 관찰하고, 이를 두 광선의 진동이 서로 상쇄되는 간섭 현상으로 설명했다.^[83] 프레넬은 내부 간섭 무늬를 장애물 양쪽 가장자리에서 나오는 원형 파동의 중첩으로, 외부 간섭 무늬를 직접파와 가장자리에서 반사된 파동(위상이 반전되었다고 가정)의 중첩으로 설명하며 간섭 무늬 경로가 쌍곡선임을 언급했다. 또한 그는 간섭 원리를 이용해 반사 및 굴절의 일반 법칙을 설명하려 시도했다.^[84] 11월에는 뉴턴 고리와 격자(투과 격자 포함)에 대한 보충 노트를 제출했다.^[85]^[86]

프레넬의 논문 검토를 맡은 아라고는 외부 간섭 무늬의 경로가 직선이 아니라는 점을 높이 평가하며 파동 이론의 증거가 될 수 있다고 격려했다.^[88] 아라고는 프레넬이 예측한 대로 얇은 유리판을 통과한 빛이 만드는 내부 간섭 무늬가 이동하는 현상을 실험으로 확인했으며, 이는 유리 속에서 빛의 속도가 느려지기 때문이라고 프레넬은 정확히 설명했다.^[95] 프레넬의 연구 결과는 1816년 5월 아라고가 공동 편집자로 있던 ''화학 및 물리학 연보''에 실렸다.^[97]^[99]

1817년, 프랑스 과학 아카데미는 회절을 주제로 물리학 ''그랑프리''를 공모했고, 아라고와 앙페르는 프레넬에게 참가를 권유했다.^[110]^[111] 프레넬은 1818년 4월 예비 노트를 통해 호이겐스 원리와 중첩 원리를 결합한 호이겐스-프레넬 원리를 제시했다. 그는 파면의 각 점에서의 진동이 이전 파면 모든 요소에서 나오는 이차 파동들의 합이며, 이 이차 파동들의 간섭 결과로 빛이 전파된다고 설명했다. 이를 바탕으로 직선 가장자리에 의한 회절 강도를 계산하기 위해 현재 프레넬 적분으로 알려진 공식을 도입하고 그 값을 표로 제시했다.^[116]^[117]

직선 가장자리의 기하학적 그림자 근처 회절 간섭 무늬. 빛의 강도는 정규화된 프레넬 적분 ''C''(''x''), ''S''(''x'') 값으로 계산되었다.

C(x) = \!\int_0^x \!\cos\big(\tfrac{1}{2}\pi z^2\big)\,dz

S(x) = \!\int_0^x \!\sin\big(\tfrac{1}{2}\pi z^2\big)\,dz\,.

1818년 7월 제출된 최종 논문에서^[119] 프레넬은 이 이론을 상세히 설명하고, 반평면, 슬릿, 좁은 띠에 의한 회절 실험 결과와 이론적 계산(프레넬 적분표 활용)이 1.5% 이내 오차로 일치함을 보였다.^[122]^[125] 이 논문은 빛의 직진성을 파동 이론으로 설명한 최초의 엄밀한 증명으로 평가받는다.^[123]

심사 위원회에는 라플라스, 비오, 푸아송 등 입자설 지지자들이 포함되어 있었지만,^[127] 프레넬의 이론은 강력했다. 특히 푸아송은 프레넬 이론에 따르면 원형 장애물 그림자 중심에 밝은 점이 나타나야 한다는 예측을 통해 이론의 허점을 찾으려 했으나, 아라고가 실험을 통해 이 푸아송 반점을 실제로 관측하면서 오히려 이론을 뒷받침하는 결정적인 증거가 되었다.^[133] 프레넬은 1819년 3월 만장일치로 그랑프리를 수상했다.^[134]^[137]

그러나 이 수상에도 불구하고 입자설 지지자들은 즉시 파동 이론으로 전향하지 않았다.^[141] 프레넬의 이론이 이차 파동의 발생 메커니즘을 명확히 설명하지 못했고,^[144] 당시 광학의 주요 관심사였던 편광 현상에 대한 설명이 부족했기 때문이다.

프레넬은 1816년부터 앙페르와의 논의를 통해 빛이 횡파 성질을 가질 수 있다는 생각을 발전시켰다. 그는 직교하는 편광된 빛이 간섭하지 않는 현상과 색 편광 현상에서 나타나는 위상 변화 규칙을 설명하기 위해 빛 파동이 순수하게 횡파라고 가정하면 가장 잘 설명된다는 결론에 도달했다.^[160]^[161] 영 역시 독립적으로 유사한 아이디어를 제시했지만,^[162] 자연광(비편광된 빛)이 어떻게 설명될 수 있는지에 대한 문제는 남아 있었다.

1821년 발표된 논문에서 프레넬은 이 문제를 해결하는 돌파구를 제시했다. 그는 자연광(비편광된 빛)이 실제로는 편광 방향이 매우 빠르고 무작위적으로 변하는 횡파들의 연속적인 중첩 상태라고 설명했다. 즉, 빛은 항상 (횡파로서) 편광되어 있지만, 그 방향이 급격히 변하기 때문에 비편광된 것처럼 보인다는 것이다.^[166] 편광 과정은 이러한 횡 진동을 만들어내는 것이 아니라, 이미 존재하는 횡 진동을 특정한 두 수직 방향으로 분해하고 분리하는 과정이라고 정의했다.^[170] 이 설명은 파동 이론과 입자 이론(선택론) 사이의 간극을 더욱 벌렸다.^[171] 순수한 횡파 가설은 빛의 매질인 에테르가 탄성 고체여야 한다는 어려운 문제를 제기했지만,^[172] 그 설명력은 매우 뛰어났다.

프레넬은 횡파 이론을 바탕으로 반사와 굴절 현상을 설명하는 정량적인 이론을 개발했다. 그는 에테르의 밀도가 매질의 굴절률 제곱에 비례한다고 가정하고, 빛의 진동을 입사면에 수직인 성분(''s'' 성분)과 평행한 성분(''p'' 성분)으로 나누었다.^[174] 1821년과 1823년에 걸쳐 발표된 논문에서 그는 에너지 보존 법칙과 경계면에서의 진동 연속성 조건을 이용하여 각 성분의 반사 및 투과 진폭(부호 포함)과 강도(세기)를 입사각과 두 매질의 굴절률 함수로 나타내는 공식을 유도했다.^[175]^[177] 이 공식들은 현재 프레넬 방정식으로 알려져 있으며, ''s'' 편광과 ''p'' 편광에 대한 반사 진폭 계수는 각각 ''프레넬의 사인 법칙''과 ''프레넬의 탄젠트 법칙''으로 불린다.^[178]

r_s=-\frac{\sin(i-r)}{\sin(i+r)}

및

r_p=\frac{\tan(i-r)}{\tan(i+r)}\,,

여기서

i

는 입사각,

r

은 굴절각이다. 프레넬은 이 공식을 통해 브루스터 각에서 ''p'' 성분의 반사율이 0이 되는 현상(반사에 의한 편광)을 설명했으며, 반사된 빛의 편광 상태 변화를 측정한 실험 결과와 이론이 1.5° 이내 오차로 일치함을 보였다.^[176] 또한 그는 계수를 복소수로 확장하여 전반사 시 ''s'' 성분과 ''p'' 성분 사이에 발생하는 위상 변화까지 설명했다.^[179] 프레넬 방정식은 이후 금속 반사 분석^[180] 및 컴퓨터 그래픽스의 물리 기반 렌더링 등 다양한 분야에 응용되었다.

1822년 논문에서 프레넬은 빛의 편광 상태를 더 세분화하여, 수직 성분의 위상이 같거나 180° 차이 나면 ''선형 편광'', 크기가 같고 1/4 주기(±90°) 위상차가 나면 ''원형 편광'', 그 외 고정된 진폭비와 위상차를 가지면 ''타원 편광''이라는 용어를 도입했다.^[181] 그는 이 개념을 이용해 광학 회전 현상을 설명했다. 선형 편광된 빛을 서로 반대 방향으로 회전하는 두 개의 원형 편광 성분으로 분해할 수 있는데, 만약 매질 속에서 두 성분의 전파 속도가 미세하게 다르면 진행 거리에 따라 두 성분 사이의 위상차가 변하게 되고, 결과적으로 합성된 선형 편광의 방향이 회전하게 된다는 것이다.^[181] 이는 편광의 '종류'가 변할 수 있음을 보여주었으며, 편광 상태에 대한 이해를 심화시켰다.^[182]

프레넬은 1817년 전반사 과정에서 빛의 편광 상태가 변하며 두 편광 성분 사이에 위상차가 발생한다는 사실을 발견했다.^[184] 그는 특정 각도에서 두 번의 전반사를 이용하면 1/4 주기의 위상차를 만들 수 있음을 알아내고, 이를 구현하기 위해 유리 평행육면체 형태의 ''프레넬 롬버스''를 고안했다. 프레넬 롬버스를 이용하면 선형 편광된 빛을 원형 편광된 빛으로 변환할 수 있으며, 그는 1823년 논문에서 이를 위한 정확한 각도를 계산했다(굴절률 1.51일 때 약 48.6° 또는 54.6°).^[185]^[186]

프레넬은 복굴절 현상, 특히 브루스터가 발견한 이축성 결정의 복잡한 복굴절 현상에도 파동 이론을 적용했다. 당시 호이겐스의 이론은 방해석과 같은 단축성 결정만 설명할 수 있었고, 비오는 말루스의 입자 이론을 바탕으로 이축성 결정에 대한 부정확한 법칙(비오의 사인 법칙, 이면각 법칙)을 제시한 상태였다.^[188]^[191]

1821년 프레넬은 토파즈 실험을 통해 이축성 결정에서는 두 개의 굴절된 광선 모두 스넬의 법칙을 따르지 않음을 보였다.^[195]^[196] 그는 빛의 속도가 방향에 따라 달라지는 것을 설명하기 위해 처음에는 3축 타원체 모델을 제안했으나,^[197] 이는 진동 방향을 정확히 예측하지 못했다. 이후 그는 파동의 법선 속도와 진동 방향을 올바르게 나타내는 4차 방정식 형태의 "탄성 표면" 개념을 도입하고,^[199] 최종적으로는 광선 속도와 파면의 형태를 정확히 기술하는 "파동 표면"의 4차 방정식을 유도했다.^[201]^[204]

\frac{x^2}{r^2-a^2} + \frac{y^2}{r^2-b^2} + \frac{z^2}{r^2-c^2} \,=\, 1\,.

(여기서

r^2 = x^2+y^2+z^2

이고

a, b, c

는 주축 방향 속도)

프레넬은 점-질량 배열 모델을 통해 매질 내에서 변위에 대해 평행한 복원력이 작용하는 세 개의 수직축이 존재함을 이론적으로 보였고,^[205] 이를 바탕으로 비오의 이면각 법칙이 특정 조건 하에서 근사적으로 성립함을 엄밀하게 증명했다.^[213] 프레넬의 연구는 이후 코시 등에 의해 비등방성 탄성체 이론 및 광학 이론으로 발전하는 기초를 마련했다.^[214] 비록 프레넬의 모델 자체는 역학적으로 완벽하지 않았지만, 다양한 광학 현상을 통합적으로 설명하고 정량적인 예측을 가능하게 함으로써 파동 이론의 승리에 결정적인 역할을 했다.^[216]

프레넬은 또한 브루스터가 발견한 광탄성 현상, 즉 투명한 물질에 응력을 가하면 복굴절이 나타나는 현상을 실험적으로 확인했다. 1822년 그는 여러 개의 유리 프리즘을 강하게 압축하여 실제로 이중상을 관찰하는 데 성공했다.^[217] 더 나아가 그는 석영과 같이 광학 활성을 가진 결정을 이용한 실험을 통해 광학 회전 현상이 본질적으로 복굴절의 특수한 형태임을 직접적으로 증명했다. 그는 특수하게 제작된 석영 프리즘을 통과한 빛이 원형 편광된 두 개의 이미지로 분리되는 것을 관찰함으로써 이를 확인했다.^[218]

3. 2. 프레넬 렌즈 발명

프레넬이 렌즈를 사용하여 등대 빔의 초점을 맞춘 첫 번째 인물은 아니었다. 1789년 런던의 유리 세공인 토마스 로저스가 포틀랜드 빌의 올드 로어 등대에 직경 53cm, 중앙 두께 14cm의 렌즈를 처음 설치했지만, 유리에 의한 빛 흡수로 많은 빛이 손실되었다.^[238]

무게와 흡수를 줄이기 위해 볼록 렌즈를 일련의 동심 환형 프리즘으로 대체하는 아이디어 역시 프레넬 이전에 존재했다. 1748년 뷔퐁 백작은 단일 유리 조각으로 이러한 프리즘을 단계별로 연마할 것을 제안했고, 1790년 콩도르세 후작은 환형 부분을 별도로 만들어 조립하는 방식을 제안했으나 당시 기술로는 실현하기 어려웠다.^[240] 이러한 초기 디자인은 등대가 아닌 태양광선 집광기를 위한 것이었다. 스코틀랜드의 데이비드 브루스터 역시 1811년에 콩도르세와 유사한 시스템을 제안하고 1820년까지 영국 등대에 사용할 것을 주장했다.

한편, 1819년 6월 21일, 프레넬은 프랑수아 아라고(1813년부터 위원회 위원)의 추천으로 등대 조명 개선 가능성을 검토하기 위한 Commission des Phares|코미시옹 데 파르^프랑스어(등대 위원회)에 임시 파견되었다.^[241] 이 위원회는 1811년 나폴레옹에 의해 설립되어 프레넬의 고용주인 코르 드 퐁(Corps des Ponts) 산하에 있었다.^[242]

1819년 8월 말, 프레넬은 이전의 제안들을 알지 못한 채, 위원회에 당시 사용되던 반사경을 대체하기 위해 lentilles à échelons|랑틸 아 에슐롱^프랑스어(단계별 렌즈)을 사용할 것을 권고했다.^[243] 기존 반사경은 입사광의 약 절반만 반사하는 단점이 있었다.^[244]^[245] 위원 중 한 명인 자크 샤를은 뷔퐁의 제안을 상기시켰으나,^[239] 뷔퐁의 렌즈는 양볼록이고 한 조각으로 된 반면, 프레넬의 렌즈는 평볼록이며 제작이 용이하도록 여러 개의 프리즘으로 구성되었다.^[239]

프레넬은 공식 예산 500FRF으로 프랑수아 솔레이에게 프로토타입 제작을 의뢰했다. 1820년 3월에 완성된 프로토타입은 한 변이 55cm인 사각형 렌즈 패널로, 97개의 다각형 프리즘을 포함하고 있었다. 위원회는 이에 깊은 인상을 받아 완전한 8개 패널 버전을 요청했고, 자금 부족에도 불구하고 1년 후 76cm 사각형 패널을 갖춘 모델이 완성되었다. 1821년 4월 13일 저녁에 열린 공개 시연에서 프레넬 렌즈는 기존 반사경을 압도하는 성능을 보여주었다.^[246]

프레넬의 다음 렌즈는 생고뱅에서 제작한 8개의 "불스아이" 패널이 있는 회전 장치였다.^[240] 이 장치는 8개의 회전하는 빔을 만들어 선원들이 주기적인 섬광으로 등대를 식별할 수 있게 했다. 각 메인 패널 위와 뒤에는 더 작고 경사진 불스아이 패널이 있어 빛을 경사진 평면 거울로 굴절시킨 후 수평으로 반사시켜 섬광의 지속 시간을 늘렸다.^[247] 메인 패널 아래에는 128개의 작은 거울이 4개의 링 형태로 배열되어 빛을 수평선으로 반사시켜 섬광 사이에 희미하지만 지속적인 빛을 제공했다.^[247] 1822년 8월 20일, 미완성된 개선문에서 열린 공식 테스트는 위원회와 루이 18세 및 그의 수행원들이 32km 떨어진 곳에서 지켜보는 가운데 성공적으로 이루어졌다. 이 장치는 겨울 동안 보르도에 보관되었다가 프레넬의 감독하에 코르두앙 등대에 다시 조립되어, 1823년 7월 25일 세계 최초의 등대용 프레넬 렌즈로 점등되었다.^[248] 이 시기 직후 프레넬의 건강이 악화되기 시작했다.^[249]

1824년 5월, 프레넬은 Commission des Phares|코미시옹 데 파르^프랑스어의 비서로 승진하여 급여를 받는 첫 위원이 되었으며, 수석 엔지니어 역할도 겸임했다.^[250]^[251] 그는 1821년부터 에콜 폴리테크니크의 시험관으로도 활동했지만, 건강 악화와 등대 작업에 집중하기 위해 1824년 말 사임했다.^[252]

같은 해, 프레넬은 빛을 수평선 주변에 고르게 퍼뜨리면서 상하 방향의 빛 손실을 최소화하는 최초의 고정 렌즈를 설계했다. 이상적인 형태는 공통 수직 축을 중심으로 하는 토러스 단면을 가진 원통형 드럼 모양이었으며, 굴절(디옵트릭) 부분 위아래에 반사(카톱트릭) 링을 추가하여 전체적으로 벌집 모양을 구상했다.^[253] 실제로 제작된 최초의 고정 렌즈는 1825년 2월 1일 던커크에 설치된 3등급 렌즈였으나, 당시 기술적 한계로 16각형 평면 구조를 가졌다.^[254]^[255]

1825년, 프레넬은 고정 렌즈 설계에 회전 배열을 추가하여, 고정된 빛의 일부를 회전 패널을 통해 좁은 빔으로 굴절시키는 방식도 고안했다.^[256] 또한 같은 해에 Carte des Phares|카르트 데 파르^프랑스어(등대 지도)를 공개하여, 51개의 등대와 항구 조명을 렌즈 크기(등급)와 섬광 특성(고정광, 분당 1회 섬광, 분당 2회 섬광 등)에 따라 체계적으로 분류했다.^[257]

1825년 말, 프레넬은 반사 요소에서의 빛 손실을 줄이기 위해 각 거울을 카타디옵트릭 프리즘으로 대체할 것을 제안했다. 이 프리즘은 빛이 첫 번째 표면에서 굴절되고, 두 번째 표면에서 전반사된 후, 세 번째 표면을 통해 다시 굴절되는 방식이다.^[259] 이는 현재 우리가 알고 있는 등대 렌즈의 기본 구조가 되었다. 1826년에는 생마르탱 운하에서 사용할 작은 모델을 조립했지만, 프레넬은 실제 크기의 카타디옵트릭 렌즈가 완성되는 것을 보지 못하고 사망했다.

프레넬 사후에도 렌즈 개발은 계속되었다. 토로이드 프리즘을 사용한 최초의 고정 렌즈는 스코틀랜드 엔지니어 앨런 스티븐슨이 레오노르 프레넬(프레넬의 동생)의 지시에 따라 설계하여 1836년 메이 섬 등대에 설치되었다.^[260] 최초의 대형 카타디옵트릭 렌즈는 1842년 그라블린과 일 비에르주 등대를 위해 제작된 3등급 고정 렌즈였다. 완전한 카타디옵트릭 구조의 1등급 렌즈는 1852년 알리(Ailly) 등대에 처음 설치되었고, 순수하게 회전하는 빔만을 가진 최초의 완전 카타디옵트릭 1등급 렌즈는 1854년 생클레망데발렌 등대에 설치되어 오귀스탱 프레넬이 구상했던 Carte des Phares|카르트 데 파르^프랑스어 계획을 완성시켰다.^[261]

뷔퐁이 구상했던 것과 유사한 단일 조각의 계단식 디옵트릭 렌즈 생산은 1852년, 코닝의 존 L. 길릴랜드가 프레스 성형 유리로 이러한 렌즈를 만드는 방법을 특허 내면서 실용화되었다. 1950년대 이후에는 플라스틱이 유리를 대체하면서 미세한 계단의 프레넬 렌즈가 오버헤드 프로젝터의 컨덴서 렌즈나 저렴한 플라스틱 시트 형태의 돋보기 등으로 널리 사용되게 되었다.^[262]

3. 3. 기타 업적

1811년 방데주 서부 지역 근무 당시, 프레넬은 암모니아 재활용을 고려하지 않았다는 점만 제외하면 현대적인 탄산나트륨 생산 방식인 솔베이 공정의 핵심 원리를 예측했다.^[26]

1815년 데이비드 브루스터는 등방성 물질에 기계적 응력을 가하면 복굴절 현상이 나타나 색상이 보이는 현상(광탄성)을 발견했다. 프레넬은 1822년, 여러 개의 프리즘을 강하게 압축하여 실제로 이중 이미지가 보이는 것을 확인함으로써 브루스터의 설명을 직접적으로 증명했다.^[217] 그는 또한 압축된 프리즘 대신 석영과 같은 광학 활성 물질을 사용하면 원형 편광된 두 개의 이미지가 생성될 것이라고 예측하고 실험으로 확인하여, 광학 회전이 복굴절의 한 형태임을 보였다.^[218]

프레넬은 전반사 과정에서 편광된 빛의 성분들 사이에 위상차가 발생한다는 사실을 발견했다.^[184] 그는 이를 이용하여 1817년, 특정 각도로 설계된 유리 평행육면체(프레넬 롬버스)를 통과시키면 선형 편광된 빛을 원형 편광이나 타원 편광으로 바꿀 수 있음을 보였다. 이는 빛의 편광 상태를 제어하는 중요한 기술적 발전을 가져왔다. 1823년에는 전반사 시 발생하는 위상 변화를 정량적으로 계산하고, 굴절률 1.51인 유리로 프레넬 롬버스를 만들기 위한 정확한 각도(약 48.6° 또는 54.6°)를 제시했다.

1818년, 프레넬은 프랑수아 아라고가 발견한 '광행차 현상이 관측자의 운동 상태와 무관하다'는 실험 결과를 설명하기 위해 에테르 끌림 가설을 제안했다. 그는 빛의 매질로 가정된 에테르가 움직이는 물체(예: 지구)에 의해 부분적으로 끌려간다고 가정했다. 구체적으로, 굴절률

n

인 물체가 속도

v

로 움직일 때, 물체 내부의 에테르는

\,v(1-1/n^2)

만큼의 속도로 끌려가 빛의 속도에 영향을 준다고 설명했다. 이 인자

(1-1/n^2)

는 프레넬 끌림 계수로 알려지게 되었다.^[288] 이 가설은 후에 특수 상대성 이론으로 이어지는 중요한 아이디어 중 하나가 되었다.

프레넬은 빛의 분산(빛의 파장에 따라 매질 속에서의 속도가 달라지는 현상)을 설명하기 위해, 매질을 이루는 입자들이 서로에게 미치는 힘이 빛의 파장과 비교할 만한 거리까지 작용한다고 가정했다.^[290] 그는 이 아이디어를 바탕으로 분산 현상을 설명하는 이론을 개발하려 했으며, 관련 원고는 사후에 발견되었다.^[291]^[292] 그의 아이디어는 이후 오귀스탱 루이 코시 등에 의해 발전되어 코시의 방정식과 같은 경험적 공식으로 이어졌고, 파동 이론이 분산 현상과 양립 가능함을 보이는 데 기여했다.^[293]^[294]

4. 수상 및 명예

다비드 당제르가 제작한 오귀스탱 프레넬 흉상(1854년). 이전에는 우르탱, 지롱드의 등대에 있었고, 현재 국립 해양 박물관에 전시되어 있다.

프레넬은 1819년 4월 파리 필로마틱 학회의 회원으로 선출되었고,^[263] 1822년에는 학회 과학 게시판의 편집자 중 한 명이 되었다.^[264]

그는 프랑스 과학 아카데미 회원 자격을 얻기 위해 노력했다. 1817년 5월 아라고의 제안으로 처음 회원 자격을 신청했지만 단 한 표만 얻었고,^[263] 당시 당선자는 조제프 푸리에였다. 1822년 11월 푸리에가 아카데미 상임 서기로 승진하면서 물리학 부문에 공석이 생겼으나, 1823년 2월 선거에서는 피에르 루이 뒬롱이 36표를 얻어 20표를 얻은 프레넬을 제치고 당선되었다. 그러나 1823년 5월, 자크 샤를의 사망으로 또 다른 공석이 생기자 프레넬은 마침내 만장일치로 아카데미 회원으로 선출되었다.^[265] 1824년에는 레지옹 도뇌르 훈장 기사 서훈을 받았다.^[266]

한편, 영국에서는 프레넬의 파동 이론이 아직 널리 받아들여지지 않았다. 1824년 11월 프레넬은 토마스 영에게 보낸 편지에서 명예에 대한 자신의 생각을 다음과 같이 밝혔다.

: 저는 영국 학자들의 칭찬에 제가 부여하는 가치를 부정할 생각은 전혀 없으며, 그들이 저에게 아첨하지 않았을 것이라고 주장할 생각도 없습니다. 그러나 오랫동안 이 감수성, 또는 영광에 대한 사랑이라고 불리는 허영심은 저에게서 많이 무뎌졌습니다. 저는 대중의 표를 얻기 위해 일하기보다는, 제 노력의 가장 달콤한 보상이었던 내면의 인정을 얻기 위해 훨씬 적게 일합니다. 의심할 여지 없이, 저는 혐오감이나 낙담의 순간에 연구를 계속하도록 자극하기 위해 허영심의 자극이 종종 필요했습니다. 그러나 MM. 아라고, 라플라스, 비오로부터 받은 모든 칭찬은 이론적 진실을 발견하고 실험으로 제 계산을 확인하는 것만큼 저에게 기쁨을 주지 못했습니다.^[267]

그러나 영국 학계의 인정은 곧 이어졌다. 1825년 6월 9일, 프레넬은 런던 왕립 학회의 외국인 회원이 되었다. 1827년 그는 "편광된 빛의 현상에 적용된 파동 이론의 개발과 물리 광학 분야의 다양한 중요한 발견"에 대한 공로를 인정받아 왕립 학회의 럼퍼드 메달을 수상했다.

프레넬 사후에도 그의 업적은 기려지고 있다. 1884년 9월 14일, 그의 출생지에 기념비가 세워졌으며, 헌정식에서는 쥘 자맹 과학 아카데미 상임 서기가 연설했다. 그의 이름 "FRESNEL"은 에펠탑에 새겨진 72인의 과학자 및 기술자 이름 중 하나로 포함되었다(남동쪽 면, 왼쪽에서 네 번째). 19세기에 프랑스의 모든 등대가 프레넬 렌즈를 채택하면서 해안 안전에 크게 기여했기 때문에, 많은 등대에 그의 흉상이 세워졌다.^[268] 또한 달의 지형인 프레넬 곶과 프레넬 열구는 그의 이름을 따서 명명되었다.

5. 평가 및 영향

프레넬의 빛에 대한 파동 이론은 당시 지배적이던 입자설(방출 이론)에 도전하며 19세기 광학 연구의 중요한 토대를 마련했다. 입자설은 빛을 입자의 이동으로 설명했지만, 반사나 굴절 외의 현상에 대해서는 정량적인 예측을 내놓기 어려웠다.^[145] 반면 프레넬은 편광 현상을 간섭 실험에 도입하는 등 파동의 관점에서 빛의 다양한 성질을 설명하고자 했다.

프레넬은 1821년 6월, ''De la Lumière''(빛에 관하여)라는 제목의 포괄적인 에세이를 완성하여 1822년 2월까지 출판했다.^[219]^[220] 이 137페이지 분량의 글은 빛의 본질, 회절, 박막 간섭, 반사와 굴절, 복굴절 및 편광, 색채 편광 등 광범위한 주제를 다루며 파동 이론을 일반 독자들에게도 알리는 계기가 되었다.^[221]

프랑스 과학 아카데미는 앙페르, 아라고, 푸리에, 푸아송에게 프레넬의 연구 검토를 맡겼다.^[222] 1822년 8월, 아라고가 주도하여 작성한 보고서^[223]가 발표되자, 당대 최고의 과학자였던 라플라스는 이 연구의 중요성을 강조하며 다음과 같이 말했다고 전해진다.

보고서가 낭독된 직후 라플라스가 연설을 시작하여… 방금 보고된 연구의 특별한 중요성을 선언했다. 그는 이 연구를 수행한 저자가 끈기와 그의 예지에 대해 축하를 보냈으며, 가장 영리한 사람조차 발견하지 못한 법칙을 발견했으며, 후세의 판단을 약간 앞서, 이 연구를 오랫동안 아카데미에 전달된 모든 것보다 높이 평가한다고 선언했다.^[225]

라플라스가 이 시점에 파동 이론을 완전히 받아들였는지에 대해서는 논란이 있지만^[226]^[227], 그의 발언은 프레넬 연구의 가치를 공식적으로 인정한 중요한 사건이었다.

빨간색 레이저 빛으로 조명된 0.09 mm 원형 구멍으로부터 떨어진 에어리 회절 패턴. 이미지 크기: 17.3 mm × 13 mm

그러나 모든 과학자가 프레넬의 이론을 즉시 받아들인 것은 아니었다. 푸아송은 에테르라는 가상의 매질에서 횡파가 존재할 수 있는지 의문을 제기하며 프레넬의 이론을 비판했다. 그는 유체 역학 방정식을 근거로 들었지만, 프레넬은 해당 방정식이 점성과 같은 기본적인 현상조차 설명하지 못한다는 점을 지적하며, 빛의 현상을 잘 설명하는 횡파 가설을 포기할 이유가 없다고 반박했다. 오히려 에테르 모델이 횡파를 수용하도록 발전해야 한다고 주장했다.^[228] 푸아송은 결국 사망 직전에 파동 이론을 받아들인 것으로 알려져 있다.^[229]

푸아송의 주저함과 달리, 프랑스 과학계에서는 프레넬의 파동 이론이 비교적 빠르게 받아들여졌다. 1820년대에 활동하기 시작한 젊은 세대의 물리학자들과 수학자들(푸이에, 사바르, 라메, 나비에, 리우빌, 코시 등)은 대부분 파동 이론을 지지했다. 프레넬의 주요 반대자였던 비오 역시 시간이 지나면서 파동 이론을 수용한 것으로 보인다.^[230]

프레넬의 이론은 프랑스를 넘어 영국과 독일 등 다른 유럽 국가로 확산되었다. 영국의 저명한 과학자 존 허셜은 1828년경 파동 이론에 매우 우호적인 글을 발표했고^[231], 토머스 영이 번역한 프레넬의 ''De la Lumière''가 1827년부터 1829년까지 연재되면서 영국 과학계에 파동 이론이 소개되었다.^[232] 케임브리지 대학교의 조지 비델 에어리는 1831년까지 파동 이론을 받아들였고, 1834년에는 파동 이론을 이용해 원형 구멍에 의한 회절 패턴(에어리 원반)을 계산하여 망원경의 분해능 한계를 설명했다. 1830년대 말 영국에서 파동 이론에 반대한 주요 인물은 브루스터 정도였는데, 그는 광화학 효과나 분산 현상을 파동 이론으로 설명하기 어렵다고 생각했다.^[234] 독일에서도 프라운호퍼와 프란츠 에른스트 노이만 등이 파동 이론을 채택하면서 점차 학계의 표준 이론으로 자리 잡았다.^[235]

과학사학자 윌리엄 휴얼은 파동 이론의 가장 큰 장점으로 '가정의 경제성'을 꼽았다. 입자설은 새로운 현상을 설명하기 위해 계속 새로운 가정이 필요했지만, 파동 이론은 하나의 가설로 여러 현상을 일관되게 설명하거나 예측할 수 있었다는 것이다.^[236] 이러한 파동 이론의 예측 능력은 1850년 푸코와 피조가 빛이 공기보다 물에서 더 느리게 이동한다는 사실을 실험적으로 증명하면서 다시 한번 확인되었다. 이는 파동 이론의 예측과 일치하는 결과였고, 입자설과는 반대되는 결과였다.^[237]

1823년 최초의 프레넬 렌즈가 사용된 코르두앙 등대의 랜턴실. 현재의 고정식 렌즈는 1854년에 설치된 것이다.

프레넬의 영향력은 이론적인 영역에만 머무르지 않았다. 그가 발명한 프레넬 렌즈는 등대 기술에 혁명을 가져왔다. 기존의 거울 반사 방식보다 훨씬 효율적으로 빛을 모으고 멀리 보낼 수 있었던 프레넬 렌즈 덕분에 해상 안전이 크게 향상되었고, 이는 해상 무역과 경제 발전에 중요한 기여를 했다. 프레넬 렌즈가 처음 제안된 지 100년도 안 되어 전 세계적으로 10,000개 이상의 등대에 이 렌즈가 설치되었다.^[296] 과학사학자 테레사 H. 레비트는 "프레넬 렌즈가 한 곳에 나타나는 순간, 그 지역은 세계 경제에 연결되었다"고 평가할 정도였다.^[297]

물리 광학의 역사에서 프레넬은 빛의 입자성을 주장한 뉴턴과 빛의 전자기적 본성을 밝힌 맥스웰 사이를 잇는 핵심적인 인물로 평가받는다. 후대의 많은 과학자들은 프레넬의 업적을 높이 평가했다.

맥컬러는 1830년에 프레넬의 복굴절 이론이 "뉴턴의 식견에 영광을 돌릴 것"이라고 썼다.
험프리 로이드는 1834년 영국 과학 진흥 협회 보고서에서 프레넬의 이론에 대해 다음과 같이 선언했다.

이제 내가 진행하려는 프레넬의 이론은 알려진 모든 현상을 포괄할 뿐만 아니라 관찰을 능가하고 나중에 완전히 검증된 결과를 예측했으므로 보편적 중력의 발견 이후 만들어진 물리 과학의 가장 훌륭한 일반화로 간주될 것입니다.^[298]

그는 1841년 강의에서는 프레넬의 횡파 이론을 "물리 과학 영역을 장식한 가장 훌륭한 구조, 뉴턴의 우주 체계만 제외하고"라고 묘사했다.

윌리엄 휴얼은 그의 저서 ''귀납 과학사''에서 하위헌스와 로버트 훅을 코페르니쿠스에, 말뤼스와 브루스터를 브라헤와 케플러에 비유하며, "영과 프레넬은 결합하여 광학 과학의 뉴턴을 구성한다"고 평가했다.^[299]

물론 프레넬의 이론은 이후 맥스웰과 아인슈타인에 의해 수정되고 보완되었다. 맥스웰은 빛 파동의 본질이 전자기적임을 밝혔고, 아인슈타인은 광전 효과를 설명하며 빛의 입자성(광자)을 다시 도입하여 파동-입자 이중성이라는 새로운 개념을 제시했다. 그러나 프레넬이 연구했던 대부분의 광학 현상(회절, 간섭, 편광 등)은 여전히 파동의 관점에서 가장 효과적으로 설명된다. 이런 이유로 1927년 천문학자 외젠 미셸 안토니아디는 프레넬을 "광학의 지배적인 인물"이라고 평가했다. 프레넬의 선구적인 연구는 빛에 대한 인류의 이해를 근본적으로 바꾸었으며, 현대 광학 기술과 과학 문명 발전에 지대한 영향을 미쳤다. 그의 과학적 탐구 정신과 혁신적인 사고는 오늘날 과학 기술 발전에도 중요한 귀감이 되고 있다.

참조

_[1] 서적 Longman Pronunciation Dictionary Pearson Longman 2008
_[2] 웹사이트 Fresnel https://www.collinsd[...]
_[3] 문서 2012
_[4] 문서 2012
_[5] 문서 2013
_[6] 문서 2008
_[7] 문서 1948
_[8] 문서 2013
_[9] 문서 1866-70
_[10] 문서 2013
_[11] 서적 L'expédition scientifique et artistique de Mésopotamie et de Médie, 1851–1855 https://gallica.bnf.[...] Libraire Ancienne Honoré Champion 1922
_[12] 문서 2009
_[13] 문서 2013
_[14] 문서 1857
_[15] 문서 2013
_[16] 문서 2013
_[17] 문서 1948
_[18] 문서 1967
_[19] 문서 2013
_[20] 문서 1911
_[21] 문서 2013
_[22] 문서 1911
_[23] 문서 1911
_[24] 문서 1990
_[25] 문서 1866-70
_[26] 문서 1967
_[27] 문서 1948
_[28] 문서 1866-70
_[29] 문서 1948
_[30] 문서 1857
_[31] 문서 2013
_[32] 문서 1690
_[33] 문서 1730
_[34] 문서 1690
_[35] 문서 2012
_[36] 서적 Darrigol, 2012
_[37] 서적 Huygens, 1690
_[38] 서적 Young, 1855
_[39] 서적 Darrigol, 2012
_[40] 서적 Darrigol, 2012
_[41] 서적 Darrigol, 2012
_[42] 서적 Huygens, 1690
_[43] 서적 Darrigol, 2012; Newton, 1730
_[44] 서적 Newton, 1730
_[45] 서적 Newton, 1730
_[46] 서적 Newton, 1730
_[47] 서적 Darrigol, 2012; Newton, 1730
_[48] 서적 Darrigol, 2012
_[49] 서적 Young, 1855
_[50] 서적 Young, 1855
_[51] 서적 Darrigol, 2012
_[52] 서적 Huygens, 1690
_[53] 서적 Newton, 1730
_[54] 서적 Newton, 1730
_[55] 서적 Newton, 1730
_[56] 서적 Newton, 1730
_[57] 서적 Frankel (1974) and Young (1855
_[58] 서적 Young, 1855
_[59] 서적 Darrigol, 2012; Silliman, 1967
_[60] 서적 Darrigol, 2012; Silliman, 1967
_[61] 서적 Young, 1855
_[62] 서적 Young, 1855
_[63] 서적 Levitt, 2009; Darrigol, 2012
_[64] 서적 Darrigol, 2012; Frankel, 1976
_[65] 서적 Buchwald, 1989; Levitt, 2009
_[66] 서적 Frankel, 1976; Buchwald, 1989; Darrigol, 2012
_[67] 서적 Frankel, 1976; Darrigol, 2012
_[68] 서적 Young, 1855
_[69] 서적 Frankel, 1976
_[70] 서적 Newton (1730)
_[71] 서적 Frankel, 1976
_[72] 서적 Buchwald, 1989
_[73] 서적 The story that Ampère lost the essay (propagated from Boutry, 1948, p. 593?) is implicitly contradicted by Darrigol (2012, p. 198), Buchwald (1989, p. 117), Mérimée's letter to Fresnel dated 20 December 1814 (in Fresnel, 1866–70, vol. 2, pp. 830–831), and two footnotes in Fresnel's collected works (Fresnel, 1866–70, vol. 1, pp. xxix–xxx, note 4, and p. 6n)
_[74] 서적 Boutry, 1948
_[75] 서적 Fresnel, 1866-70
_[76] 서적 Fresnel, 1866-70
_[77] 서적 Fresnel, 1866-70
_[78] 서적 Buchwald, 1989
_[79] 서적 Levitt, 2013
_[80] 서적 Kipnis, 1991
_[81] 서적 Darrigol, 2012
_[82] 서적 Young's book https://archive.org/[...]
_[83] 서적 Darrigol, 2012
_[84] 서적 Buchwald, 1989
_[85] 서적 Darrigol, 2012
_[86] 서적 Fresnel, 1866-70
_[87] 서적 Frankel, 1976
_[88] 서적 Fresnel, 1866-70
_[89] 서적 Buchwald, 1989
_[90] 서적 Young, 1807
_[91] 서적 Young to Arago 1817-01-12
_[92] 서적 Newton, 1730
_[93] 서적 Kipnis, 1991
_[94] 서적 Silliman, 1967
_[95] 서적 Silliman, 1967
_[96] 서적 Silliman (1967, p. 163) and Frankel (1976, p. 156) give the date of Arago's note on scintillation as 1814; but the sequence of events implies 1816, in agreement with Darrigol (2012, pp. 201, 290). Kipnis (1991, pp. 202–203, 206) proves the later date and explains the origin and propagation of the incorrect earlier date.
_[97] 서적 Fresnel, 1816
_[98] 서적 Darrigol, 2012
_[99] 서적 Kipnis, 1991
_[100] 서적 Kipnis, 1991
_[101] 서적 Cf. Young, 1807
_[102] 서적 Darrigol, 2012
_[103] 서적 Fresnel, 1866-70
_[104] 서적 Silliman, 1967
_[105] 서적 Buchwald, 1989
_[106] 서적
_[107] 서적
_[108] 서적
_[109] 서적
_[110] 서적
_[111] 서적
_[112] 서적
_[113] 서적
_[114] 서적
_[115] 서적
_[116] 서적
_[117] 서적
_[118] 서적
_[119] 서적
_[120] 서적
_[121] 서적
_[122] 서적
_[123] 서적
_[124] 서적
_[125] 서적
_[126] 서적
_[127] 서적
_[128] 서적
_[129] 서적
_[130] 서적
_[131] 서적
_[132] 서적
_[133] 서적
_[134] 서적
_[135] 서적
_[136] 서적
_[137] 서적
_[138] 서적
_[139] 서적
_[140] 서적
_[141] 문서
_[142] 서적
_[142] 서적
_[143] 서적
_[143] 서적
_[144] 서적
_[144] 서적
_[144] 서적
_[145] 서적
_[145] 서적
_[146] 서적
_[146] 서적
_[146] 서적
_[147] 서적
_[148] 서적
_[148] 서적
_[149] 서적
_[150] 서적
_[151] 서적
_[152] 서적
_[153] 서적
_[153] 서적
_[154] 간행물
_[155] 서적
_[155] 서적
_[156] 서적
_[157] 서적
_[158] 서적
_[159] 서적
_[159] 서적
_[159] 서적
_[160] 서적
_[161] 간행물
_[161] 서적
_[161] 서적
_[161] 서적
_[162] 서적
_[163] 서적
_[163] 간행물
_[164] 서적
_[165] 서적
_[166] 서적
_[166] 서적
_[167] 서적
_[167] 서적
_[168] 서적
_[169] 서적
_[169] 서적
_[170] 서적
_[170] 서적
_[171] 서적
_[172] 서적
_[172] 서적
_[172] 서적
_[173] 서적
_[173] 서적
_[174] 문서
_[175] 서적
_[175] 서적
_[176] 서적 Buchwald, 1989, pp. 390–391; Fresnel, 1821a, §§ 20–22
_[177] 서적 Buchwald, 1989, pp. 391–393; Whittaker, 1910, pp. 133–135
_[178] 서적 Whittaker, 1910, p. 134; Darrigol, 2012, p. 213; Fresnel, 1866–70, vol. 1, pp. 773, 757
_[179] 서적 Buchwald, 1989, pp. 393–394; Whittaker, 1910, pp. 135–136; Fresnel, 1866–70, vol. 1, pp. 760–761, 792–796
_[180] 서적 Whittaker, 1910, pp. 177–179; Buchwald, 2013, p. 467
_[181] 서적 Buchwald, 1989, pp. 230–232, 442
_[182] 서적 Cf. Buchwald, 1989, p. 232
_[183] 서적 Lloyd, 1834, p. 368
_[184] 서적 Darrigol, 2012, p. 207
_[185] 서적 Buchwald, 1989, pp. 223, 336; on the latter page, a "prism" means a Fresnel rhomb or equivalent. A footnote in the 1817 memoir (Fresnel, 1866–70, vol. 1, p. 460, note 2) described the emulator more briefly, and not in a self-contained manner
_[186] 서적 Fresnel, 1818a, especially pp. 47–49
_[187] 서적 Jenkins & White, 1976, pp. 576–579 (§ 27.9, esp. Fig. 27M)
_[188] 서적 Buchwald, 1989, pp. 254–255, 402
_[189] 서적 Cf. Buchwald, 1989, p. 269
_[190] 서적 Grattan-Guinness, 1990, p. 885
_[191] 서적 Buchwald, 1989, pp. 269, 418
_[192] 간행물 Cf. Fresnel, 1822a, tr. Young, in ''Quarterly Journal of Science, Literature, and Art'', Jul.– Dec. 1828, at pp. 178–179 https://books.google[...]
_[193] 서적 Buchwald, 1989, p. 260
_[194] 문서 In Fresnel's collected works (1866–70), a paper is said to have been "presented" ("présenté") if it was merely delivered to the Permanent Secretary of the Académie for witnessing or processing (cf. vol. 1, p. 487; vol. 2, pp. 261, 308). In such cases this article prefers the generic word "submitted", to avoid the impression that the paper had a formal reading
_[195] 서적 Printed in Fresnel, 1866–70, vol. 2, pp. 261–308
_[196] 서적 Silliman, 1967, pp. 243–246 (first experiment); Buchwald, 1989, pp. 261–267 (both experiments). The first experiment was briefly reported earlier in Fresnel, 1821c
_[197] 서적 Buchwald (1989, pp. 267–272) and Grattan-Guinness (1990, pp. 893–894 call it the "ellipsoid of elasticity"
_[198] 서적 Buchwald, 1989, pp. 267–272; Grattan-Guinness, 1990, pp. 885–887
_[199] 서적 Buchwald, 1989, pp. 274–279
_[200] 서적 Buchwald, 1989, pp. 279–280
_[201] 문서 Literally "surface of the wave"—as in Hobson's translation of Fresnel 1827
_[202] 서적 Fresnel, 1866–70, vol. 2, pp. 340, 361–363; Buchwald, 1989, pp. 281–283. The derivation of the "wave surface" ''from'' its tangent planes was eventually accomplished by Ampère in 1828 (Lloyd, 1834, pp. 386–387; Darrigol, 2012, p. 218; Buchwald, 1989, pp. 281, 457)
_[203] 서적 Fresnel, 1866–70, vol. 2, pp. 369–442
_[204] 서적 Buchwald, 1989, pp. 283–285; Darrigol, 2012, pp. 217–218; Fresnel, 1866–70, vol. 2, pp. 386–388
_[205] 서적 Grattan-Guinness, 1990, pp. 891–892; Fresnel, 1866–70, vol. 2, pp. 371–379
_[206] 서적 Buchwald, 1989, pp. 285–286; Fresnel, 1866–70, vol. 2, p. 396
_[207] 서적 Grattan-Guinness, 1990, pp. 896–897. Silliman, 1967, pp. 262–263; 2008, p. 170
_[208] 서적 Buchwald, 1989, pp. 286–287, 447
_[209] 서적 Fresnel, 1827
_[210] 서적 Fresnel, 1866–70, vol. 2, p. 800n. Although the original publication (Fresnel, 1827) shows the year "1824" in selected page footers, it is known that Fresnel, slowed down by illness, did not finish the memoir until 1826 (Buchwald, 1989, pp. 289, 447, citing Fresnel, 1866–70, vol. 2, p. 776n)
_[211] 서적 Fresnel, 1827, tr. Hobson, pp. 266–273.
_[212] 서적 Fresnel, 1827, tr. Hobson, pp. 281–285.
_[213] 서적 Fresnel, 1827, tr. Hobson, pp. 320–322; Buchwald, 1989, p. 447.
_[214] 간행물 Grattan-Guinness, 1990, pp. 1003–1009,{{tsp}}1034–1040,{{tsp}}1043; Whittaker, 1910, pp. 143–145; Darrigol, 2012, p. 228.
_[215] 간행물 Whittaker, 1910, chapter {{serif|V}}; Darrigol, 2012, chapter 6; Buchwald, 2013, pp. 460–464.
_[216] 서적 Fresnel, 1827, tr. Hobson, pp. 273–281; Silliman, 1967, p. 268n; Buchwald, 1989, p. 288.
_[217] 서적 Whewell, 1857, pp. 355–356.
_[218] 간행물 Fresnel, 1866–70, vol. 1, pp. 737–739 (§4).
_[219] 논문 Fresnel, 1822a.
_[220] 서적 Grattan-Guinness, 1990, p. 884.
_[221] 서적 Cf. Frankel, 1976, p. 169.
_[222] 간행물 Fresnel, 1866–70, vol. 2, pp. 261n,{{px2}}369n.
_[223] 간행물 Printed in Fresnel, 1866–70, vol. 2, pp. 459–464.
_[224] 서적 Buchwald, 1989, p. 288.
_[225] 간행물 Fresnel, 1866–70, vol. 1, pp. lxxxvi–lxxxvii; Grattan-Guinness, 1990, p. 896.
_[226] 서적 Grattan-Guinness, 1990, p. 898.
_[227] 서적 Buchwald, 1989, pp. 289–390.
_[228] 서적 Frankel, 1976, pp. 170–171; cf. Fresnel, 1827, tr. Hobson, pp. 243–244,{{tsp}}262.
_[229] 간행물 Silliman, 1967, pp. 284–285, citing Fresnel, 1866–70, vol. 1, p. lxxxix, note 2.
_[230] 서적 Frankel, 1976, pp. 173–174.
_[231] 서적 Buchwald, 1989, pp. 291–296; Darrigol, 2012, pp. 220–221,{{tsp}}303.
_[232] 논문 Fresnel, 1822a; Kipnis, 1991, pp. 227–228.
_[233] 서적 Buchwald, 1989, p. 296.
_[234] 서적 Darrigol, 2012, pp. 222–223,{{tsp}}248.
_[235] 서적 Kipnis, 1991, pp. 225,{{px2}}227; Darrigol, 2012, pp. 223,{{px2}}245.
_[236] 서적 Whewell, 1857, pp. 340–341
_[237] 간행물 Whewell, 1857, pp. 482–483; Whittaker, 1910, p. 136; Darrigol, 2012, p. 223.
_[238] 서적 Levitt, 2013, p.{{nnbsp}}57.
_[239] 서적 Levitt, 2013, p. 59.
_[240] 서적 Levitt, 2013, p. 71.
_[241] 간행물 Levitt, 2013, pp. 51,{{px2}}53; Fresnel, 1866–70, vol. 1, p. xcvii, and vol. 3, p. xxiv.
_[242] 서적 Levitt, 2013, pp. 49–50.
_[243] 간행물 Fresnel, 1866–70, vol. 3, pp. 5–14
_[244] 서적 Levitt, 2013, pp. 56,{{px2}}58.
_[245] 간행물 Another report by Fresnel, dated 29 August 1819 (Fresnel, 1866–70, vol. 3, pp. 15–21), concerns tests on reflectors, and does not mention stepped lenses except in an unrelated sketch on the last page of the manuscript. The minutes of the meetings of the Commission go back only to 1824, when Fresnel himself took over as Secretary (Fresnel, 1866–70, vol. 3, p. 6n). Thus, unfortunately, it is not possible to ascertain the exact date on which Fresnel formally recommended ''lentilles à échelons''.
_[246] 서적 2013
_[247] 서적 1822
_[248] 서적 2009
_[249] 서적 2013
_[250] 서적 2013
_[251] 서적 2009
_[252] 서적 1990
_[253] 서적 2009
_[254] 서적 2013
_[255] 서적 2009
_[256] 서적 2009
_[257] 서적 2013
_[258] 서적 2009
_[259] 서적 2013
_[260] 서적 2009
_[261] 서적 2013
_[262] 간행물 New developments in audio-visual materials 1952-04-01
_[263] 서적 1991
_[264] 서적 1976
_[265] 서적 1990
_[266] 서적 2013
_[267] 서적 1855
_[268] 서적 2013
_[269] 서적 2013
_[270] 서적 1948
_[271] 서적 1866-70
_[272] 서적 1948
_[273] 서적 2013
_[274] 서적 1866-70
_[275] 서적 1989
_[276] 논문 1818
_[277] 서적 1991
_[278] 서적 1852
_[279] 서적 1989
_[280] 서적 1990
_[281] 문헌 Whittaker, 1910, p. 125n.
_[282] 문헌 Boutry, 1948, pp. 603–604; Fresnel, 1866–70, vol. 1, pp. i–vii.
_[283] 문헌 Silliman, 2008, p. 171.
_[284] 문헌 Buchwald, 1989, p. 116.
_[285] 문헌 Fresnel, 1866–70, vol. 2, pp. 768n, 802.
_[286] 문헌 Fresnel, 1866–70, vol. 2, p. 803n. Grattan-Guinness (1990, p. 884n) gives the year of composition as 1825, but this does not match the primary sources.
_[287] 문헌 Cf. Darrigol, 2012, pp. 258–260.
_[288] 문헌 Fresnel, 1818c.
_[289] 문헌 Darrigol, 2012, p. 212; Fresnel, 1821a, §§ 14, 18.
_[290] 문헌 Darrigol, 2012, p. 246; Buchwald, 1989, pp. 307–308; Fresnel, 1822a, tr. Young, in Quarterly Journal of Science, Literature, and Art, Jan.–Jun. 1828, at pp. 213–215. Whittaker, 1910, p. 132; Fresnel, 1866–70, vol. 2, p. 438. https://books.google[...]
_[291] 문헌 Fresnel, 1827, tr. Hobson, pp. 277n, 331n; Lloyd, 1834, p. 316.
_[292] 문헌 Fresnel, 1866–70, vol. 1, p. xcvi.
_[293] 문헌 Whittaker, 1910, pp. 182–183; Whewell, 1857, pp. 365–367; Darrigol, 2012, pp. 246–249.
_[294] 문헌 Darrigol, 2012, p. 252.
_[295] 문헌 Lloyd, 1834, pp. 387–388.
_[296] 문헌 Levitt, 2013, p. 19.
_[297] 문헌 Levitt, 2013, p. 8.
_[298] 문헌 Lloyd, 1834, p. 382.
_[299] 문헌 Whewell, 1857, pp. 370–371.
_[300] 웹사이트 フレネル https://kotobank.jp/[...]
_[301] 웹사이트 Fresnel; Augustin Jean (1788 - 1827) 2012-03-25

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com